How to calculate Treynor ratio for perpetual futures_0
How to calculate Treynor ratio for perpetual futures_1
How to calculate Treynor ratio for perpetual futures_2

====================================================

Introduction

In the evolving world of derivatives, perpetual futures have become a cornerstone instrument for both retail and institutional investors. Unlike traditional futures, they have no expiration date and are heavily influenced by funding rates, leverage dynamics, and continuous price adjustments. For traders aiming to evaluate risk-adjusted performance, the Treynor ratio stands out as a powerful metric.

This article serves as a comprehensive guide on how to calculate the Treynor ratio for perpetual futures, while also exploring strategies, practical applications, and industry insights. We will break down methodologies, compare approaches, provide FAQs, and integrate real-world practices to ensure that both beginners and professionals can benefit.

By the end, you’ll understand not just the calculation but also the interpretation, optimization, and use cases of the Treynor ratio in perpetual futures trading.

What is the Treynor Ratio?

The Treynor ratio, developed by Jack Treynor in the 1960s, measures how much excess return an investment generates per unit of systematic risk (beta). It is particularly valuable for leveraged instruments such as perpetual futures, where risk-adjusted evaluation is critical.

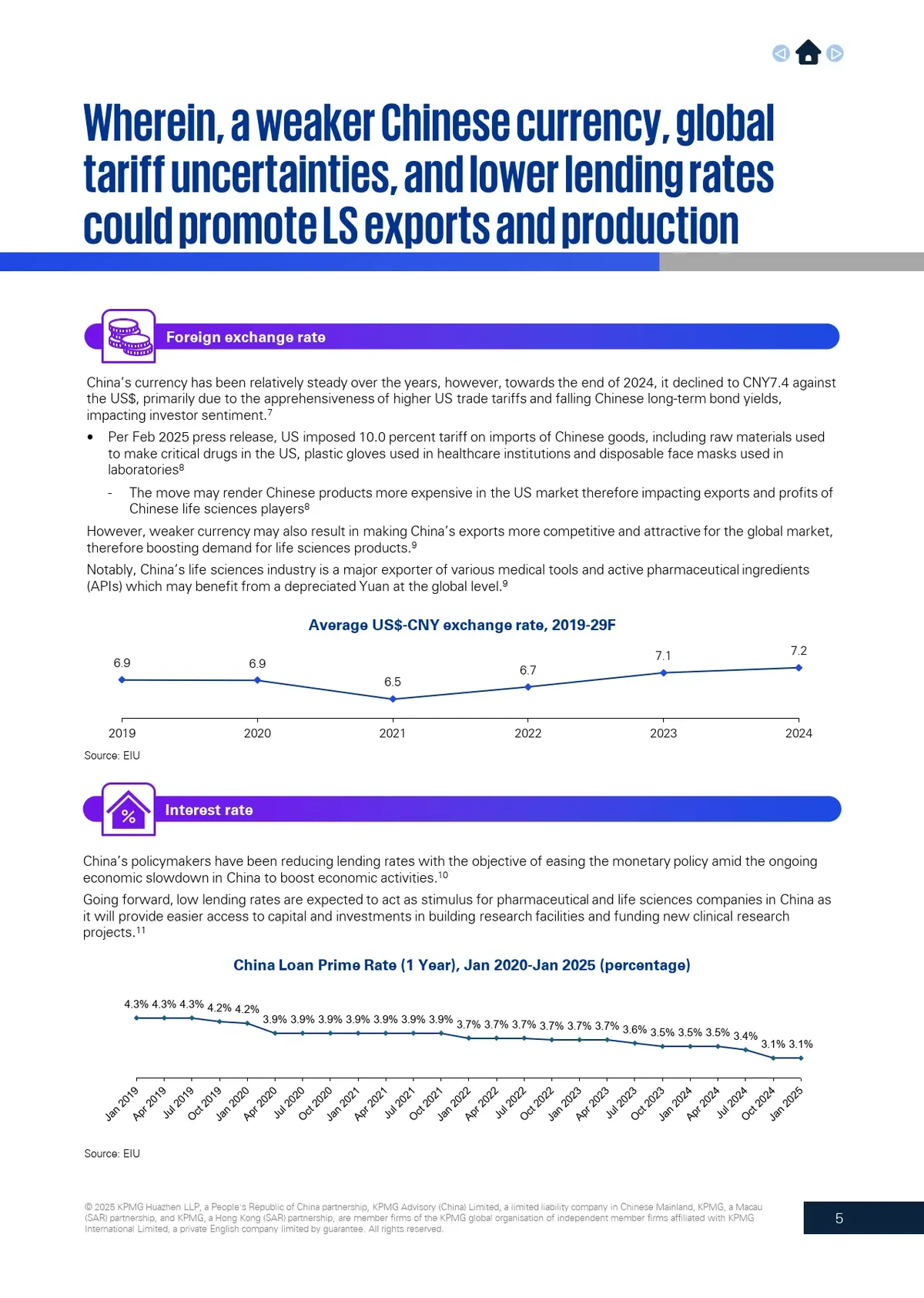
Formula for Treynor Ratio

Treynor Ratio=Rp−RfβpTreynor \ Ratio = \frac{R_p - R_f}{\beta_p}Treynor Ratio=βp​Rp​−Rf​​

Where:

  • RpR_pRp​ = Portfolio (or strategy) return
  • RfR_fRf​ = Risk-free rate
  • βp\beta_pβp​ = Beta of the portfolio relative to the market

In perpetual futures trading, RpR_pRp​ would be your strategy return, adjusted for funding payments and leverage, while βp\beta_pβp​ measures systematic risk exposure to the broader market (e.g., Bitcoin index for BTC perpetual futures).

Why Apply Treynor Ratio to Perpetual Futures?

Perpetual futures markets are highly leveraged, volatile, and funding-driven. Simple return calculations don’t reflect true performance. The Treynor ratio helps by:

  • Standardizing returns relative to risk.
  • Allowing comparison between strategies (scalping, hedging, arbitrage).
  • Supporting institutional reporting with risk-adjusted benchmarks.

This makes it an essential tool for hedge funds, quant desks, and advanced retail traders.

Step-by-Step Guide: How to Calculate Treynor Ratio for Perpetual Futures

Step 1: Gather Performance Data

  • Daily or hourly returns from perpetual futures trading strategy.
  • Adjust returns for funding fees, commissions, and slippage.
  • Example: A BTC perpetual futures strategy returns 15% in a quarter after costs.

Step 2: Define Risk-Free Rate

  • Use the U.S. Treasury bill yield or stablecoin lending rate (if calculating in crypto).
  • Suppose Rf=2%R_f = 2\%Rf​=2%.

Step 3: Estimate Beta (β\betaβ)

  • Calculate covariance of strategy returns with benchmark index (e.g., BTC spot index).
  • Divide by variance of the benchmark.

β=Cov(Rp,Rm)Var(Rm)\beta = \frac{Cov(R_p, R_m)}{Var(R_m)}β=Var(Rm​)Cov(Rp​,Rm​)​

  • Example: Beta = 1.3, indicating higher market sensitivity.

Step 4: Plug Into Formula

Treynor Ratio=15%−2%1.3=10%Treynor \ Ratio = \frac{15\% - 2\%}{1.3} = 10\%Treynor Ratio=1.315%−2%​=10%

This means the strategy generates 10% excess return per unit of market risk, a strong performance in perpetual futures trading.

Two Different Approaches to Treynor Ratio in Perpetual Futures

1. Historical Data-Based Calculation

  • Uses past return series.
  • Pros: Simple, transparent, data-rich.
  • Cons: Backward-looking, may fail in new market regimes.

2. Forward-Looking Simulation with Monte Carlo or Factor Models

  • Incorporates stress testing, scenario analysis, and simulated beta shocks.
  • Pros: Captures tail risks, future-oriented.
  • Cons: Computationally heavy, requires advanced modeling.

👉 Recommendation: Combine both methods — use historical Treynor ratio for validation and forward-looking simulation for proactive adjustments.

Example Case Study: Treynor Ratio in BTC Perpetual Futures

Imagine two traders running BTC perpetual futures strategies:

  • Trader A (High-Leverage Scalper):

    • Returns: 25%
    • Beta: 2.1
    • Treynor Ratio = (25% - 2%) / 2.1 ≈ 10.95%

  • Trader B (Market-Neutral Arbitrageur):

    • Returns: 12%
    • Beta: 0.5
    • Treynor Ratio = (12% - 2%) / 0.5 = 20%

Insight: Trader B, though generating lower nominal returns, delivers superior risk-adjusted performance.

How Does Treynor Ratio Affect Perpetual Futures Decisions?

The Treynor ratio can influence strategy choice:

  • A high ratio suggests efficient risk-taking → scaling up position sizes is justifiable.
  • A low ratio signals inefficient exposure → rebalancing or hedging is necessary.
  • For institutional desks, the Treynor ratio provides a standardized reporting tool to compare quant models across markets.

Common Pitfalls When Calculating Treynor Ratio

  1. Ignoring Funding Payments → Overstates returns.
  2. Using Wrong Benchmark → Distorts beta. BTC spot vs. perpetual index can diverge.
  3. Short Sample Periods → Beta estimates become unstable.
  4. Confusing Treynor Ratio with Sharpe Ratio → Treynor focuses only on systematic risk, while Sharpe accounts for total volatility.

Advanced Considerations

  • Multi-Asset Portfolios: Apply Treynor ratio to ETH, SOL, and BTC perpetuals simultaneously for portfolio-level insights.
  • Hedging Applications: Evaluate effectiveness of delta-neutral or basis trades with Treynor ratio.
  • Algorithmic Execution: Integrate Treynor ratio monitoring in live bots to adjust leverage dynamically.

This ties into the broader concept of optimizing Treynor ratio for perpetual futures, ensuring strategies evolve with market microstructure.

Visual Example

Treynor ratio applied to BTC perpetual futures, comparing scalping vs. arbitrage strategies.

FAQ: How to Calculate Treynor Ratio for Perpetual Futures

1. Is Treynor ratio better than Sharpe ratio for perpetual futures?

Yes, especially when leverage amplifies systematic market risk. Sharpe ratio penalizes all volatility, including idiosyncratic noise, while Treynor isolates beta-driven risks, making it more relevant for perpetuals linked to market indices.

2. What benchmark should I use for calculating beta in perpetual futures?

The best practice is to use the underlying spot index (e.g., BTC index for BTC perpetual futures). Using perpetual prices directly can distort beta due to funding mechanics.

3. How often should I recalculate Treynor ratio for my strategy?

  • Retail traders: Monthly or quarterly.
  • Institutional desks: Weekly or even daily, integrated into dashboards.
    Frequent recalculations capture shifts in funding rates, leverage, and volatility regimes.

Conclusion

Understanding how to calculate Treynor ratio for perpetual futures is essential for both professional and retail investors. By incorporating historical calculations and forward-looking simulations, traders can evaluate strategies on a true risk-adjusted basis.

The Treynor ratio is not just a number—it is a decision-making compass that impacts leverage, hedging, and scaling strategies in volatile perpetual futures markets.

If you found this guide valuable, share it with your trading peers, comment with your own Treynor ratio experiences, and let’s grow this conversation in the trading community.

Would you like me to create an Excel template or Python script that automates the Treynor ratio calculation for perpetual futures, so readers can apply it instantly to their own strategies?