
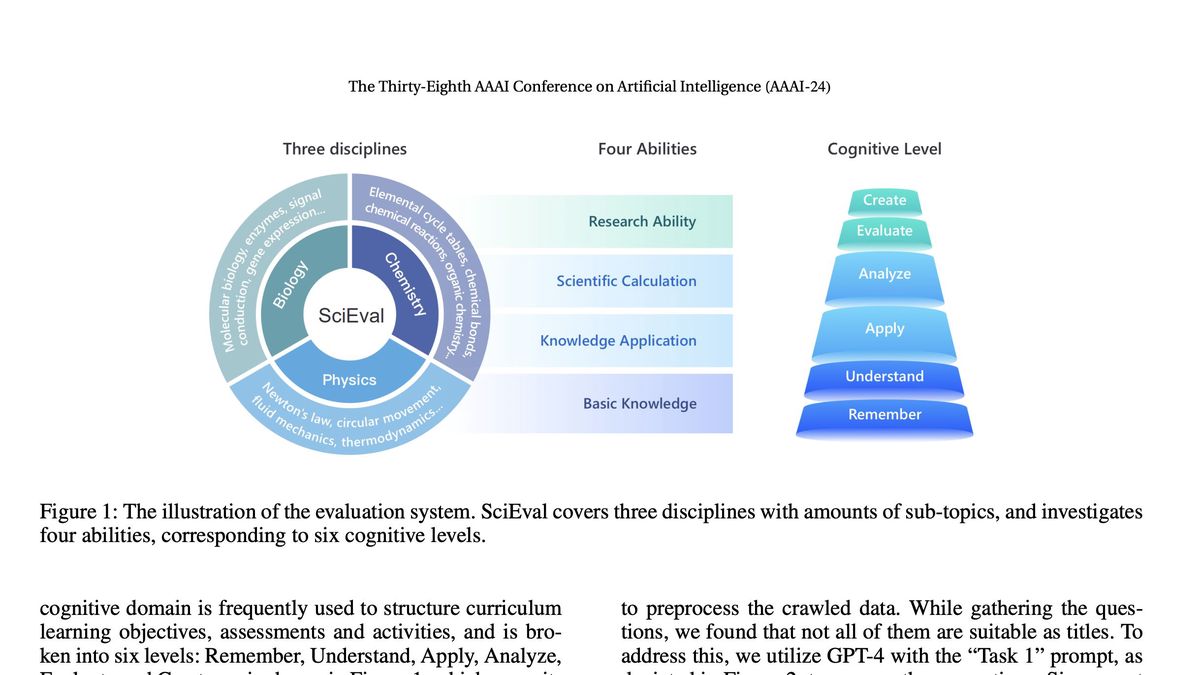

=====================================================================
The Treynor ratio is a powerful risk-adjusted performance metric that can provide invaluable insights for traders in the high-stakes world of perpetual futures. Understanding practical examples of Treynor ratio applications in perpetual futures allows traders—from retail investors to institutional professionals—to optimize strategies, balance risk exposure, and improve portfolio returns. This article offers a comprehensive, step-by-step guide on leveraging the Treynor ratio effectively in perpetual futures markets.
Understanding the Treynor Ratio in Perpetual Futures
What is the Treynor Ratio?
The Treynor ratio measures the return earned in excess of the risk-free rate per unit of systematic risk (beta). Unlike other risk metrics, it focuses on market-related risk rather than total volatility.
Treynor Ratio=Rp−Rfβp\text{Treynor Ratio} = \frac{R_p - R_f}{\beta_p}Treynor Ratio=βpRp−Rf
Where:
- RpR_pRp = Portfolio return
- RfR_fRf = Risk-free rate
- βp\beta_pβp = Beta of the portfolio
This metric is particularly suitable for perpetual futures because these instruments often exhibit high beta due to leverage and market volatility.
Why the Treynor Ratio Matters for Perpetual Futures
- Risk-Adjusted Performance: Evaluates how much return is achieved relative to market risk.
- Strategy Comparison: Helps traders compare different perpetual futures strategies under consistent risk metrics.
- Portfolio Optimization: Guides allocation toward positions that offer the best risk-return trade-off.
Integrating the Treynor ratio into analysis enables traders to make more informed decisions, particularly in volatile crypto or commodity perpetual futures markets.
Illustration of Treynor ratio comparing two perpetual futures strategies
Method 1: Evaluating Individual Perpetual Futures Positions
Step 1: Calculating Beta for a Futures Contract
- Determine historical returns of the perpetual futures contract and the relevant market index
- Use regression analysis to calculate beta (βp\beta_pβp)
Step 2: Measuring Returns Relative to Risk-Free Rate
- Calculate daily, weekly, or monthly returns of the futures contract
- Subtract the risk-free rate to obtain excess returns
Step 3: Computing the Treynor Ratio
- Divide the excess return by beta to quantify the risk-adjusted performance
- Compare ratios across different contracts or strategies
Advantages: Allows precise evaluation of individual trades or contracts
Limitations: Requires accurate market beta and stable risk-free benchmarks
Embedding these calculations into trading dashboards helps traders monitor performance dynamically.
Practical Example
- Trader A holds a BTC perpetual futures contract with beta = 1.8
- Excess return over risk-free rate = 12%
- Treynor ratio = 12% / 1.8 ≈ 6.67% per unit of market risk
This indicates a strong risk-adjusted return compared to other contracts with lower ratios.
Method 2: Portfolio-Level Treynor Ratio for Perpetual Futures
Step 1: Aggregate Portfolio Beta
- Weighted beta calculation considering each position’s exposure
- Focus on market sensitivity of the entire portfolio rather than individual contracts
Step 2: Portfolio Excess Return Calculation
- Aggregate weighted returns of all positions
- Subtract risk-free rate to get portfolio-level excess returns
Step 3: Compute Portfolio Treynor Ratio
- Divide portfolio excess return by aggregate beta
- Use results for strategy optimization and risk allocation
Portfolio-level Treynor ratio applied to multiple perpetual futures positions
Comparing Strategies Using Treynor Ratio
- Strategy X: High beta, high returns, Treynor ratio = 7%
- Strategy Y: Low beta, moderate returns, Treynor ratio = 6%
Although Strategy X is riskier, its higher Treynor ratio indicates better risk-adjusted performance, guiding professional traders to prioritize it under market-neutral risk management.
This demonstrates how upgrading strategies affect Treynor ratio in perpetual futures, enabling traders to optimize allocation based on systematic risk.
Advanced Applications
Scenario Analysis
- Simulate different market conditions (bullish, bearish, sideways)
- Evaluate Treynor ratio under stress scenarios to ensure strategies maintain positive risk-adjusted returns
Strategy Tuning
- Adjust leverage and contract exposure to optimize the Treynor ratio
- Incorporate hedging instruments to reduce beta while maintaining returns
Benefits: Enhances portfolio robustness in volatile markets
Drawbacks: Requires advanced tools and backtesting frameworks
Treynor Ratio for Retail vs. Institutional Investors
| Investor Type | Application | Complexity |
|---|---|---|
| Retail Investors | Evaluate single contracts, monitor risk-adjusted returns | Low–Moderate |
| Institutional Investors | Portfolio-level optimization, multi-strategy comparison | High |
Using Treynor ratio insights for institutional portfolios helps balance risk across multiple perpetual futures markets, ensuring capital efficiency and regulatory compliance.
Common Mistakes with Treynor Ratio
- Ignoring Beta Accuracy: Misestimating beta can distort results
- Overlooking Market Shifts: Historical beta may not reflect current volatility
- Neglecting Leverage Effects: High leverage inflates beta and affects interpretation
Applying Treynor ratio best practices ensures meaningful risk-adjusted evaluations.
FAQ
Q1: How do you calculate Treynor ratio for perpetual futures?
A1: Calculate portfolio or contract returns, subtract the risk-free rate, then divide by beta. Detailed step-by-step methods are covered in how to calculate Treynor ratio for perpetual futures guides.
Q2: Can retail traders benefit from Treynor ratio analysis?
A2: Absolutely. Retail investors can compare individual contracts or small portfolios to identify the most efficient risk-return positions, even with limited capital.
Q3: What is the main advantage of using Treynor ratio over other metrics like Sharpe ratio?
A3: Treynor ratio isolates systematic market risk, making it ideal for leveraged and beta-sensitive instruments like perpetual futures. It highlights performance per unit of market risk rather than total volatility.
Conclusion
Practical applications of the Treynor ratio in perpetual futures provide traders with quantitative insight into risk-adjusted returns, enabling better portfolio management, strategy optimization, and capital allocation. By analyzing individual contracts, evaluating portfolios, and applying advanced scenario analyses, both retail and professional traders can make informed, strategic decisions. Incorporate these methods into your trading workflow and share experiences to foster a community of informed perpetual futures traders.